problema 77 - Resolvido - Raciocínio Lógico Matemático
Para um grupo de funcionários, uma empresa oferece cursos para somente dois idiomas estrangeiros: inglês e espanhol. Há 105 funcionários que pretendem estudar inglês, 118 que preferem espanhol e 37 que pretendem estudar simultaneamente os dois idiomas. Se 1/7 do total de funcionários desse grupo não pretende estudar qualquer idioma estrangeiro, então o número de elementos do grupo é
(A) 245 (B) 238 (C) 231 (D) 224 (E))217
Solução:
Sejam os conjuntos:
I – “o conjunto dos alunos de inglês”
E – “o conjunto doa alunos de espanhol”
Seja x o total de funcionários do grupo.
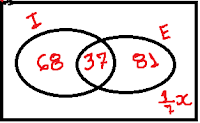
Alunos que estudam apenas inglês: 105-37 = 68 alunos
Alunos que estudam apenas espanhol: 118-37 = 81 alunos
Alunos que estudam ambas as matérias: 37 alunos
Como x/7 não pretendem estudar qualquer idioma, concluímos que 6x/7 pretendem estudar algum idioma. Logo:
Opção correta: E




Olá! Por favor, pode me explicar de onde surgiu o seis? Obrigada
ResponderExcluirOlá! Por favor, pode me explicar de onde surgiu o seis? Obrigada
ResponderExcluirTotal 7/7 menos 1/7 igaul 6/7
ResponderExcluirNão entnedi. Esse 6 aparece do nada ;/
ResponderExcluircomo o nenhum é 1/7
ResponderExcluirconclui-se que a fração toda corresponde a 7/7
portanto 6/7 é o valor da soma dos elementos dos dois conjuntos que é igual a 186 ou 6/7 do total
1/7 + 6/7 = 7/7
espero ter ajudado
Eu não entendi , da onde sai o 6 ?
ResponderExcluir